Transformer相关——(4)Poisition encoding
Transformer相关——(4)Poisition encoding
引言
上一篇总结完了attention机制,其中提到Transformer中的self-attention机制可以并行化但是缺乏位置信息,各个位置完全没有任何差别,这导致了什么问题呢?比如在一个句子中,某一个词汇它是放在句首的,那它是动词的可能性可能就比较低,这种位置信息可能在NLP的命名实体识别任务中很有用。
positional encoding位置编码就可以补充上述这类位置信息。
Poisition encoding
Poisition encoding应用在哪
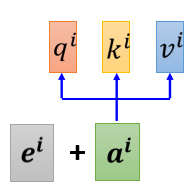
Poisition encoding位置编码机制为每一个位置设定一个 vector,叫做 positional vector(\(e^i\)),不同的位置都有一个它专属的位置编码,然后把\(e^i\)加到\(a^i\)上,再做self-attention操作。
怎么设计Poisition encoding
Poisition encoding是人工设计的,最好能满足以下条件:保证值域固定,且不同长度文本,相差相同字数,差相同值,不同顺序(方向)含义不同。
总的来说可以分为两种类型:函数型和表格型。
- 表格型:建立一个长度为L的词表,按词表的长度来分配位置id
- 函数型:通过输入token位置信息,得到相应的位置编码
表格型
位置直接作为编码,\([1,2,3..n]\)
这样的问题很明显,没有上界。过大的位置embeding,跟词embeding相加,很容易导致词向量本身含义的丢失。位置向量值不要太大,最好在限定在一个区间内。
位置编码后进行归一化,\([0,1/n,2/n,....1]\)
这样词向量的区间就变成[0,1]且具有可比性了,但是在长文本和短文本的的情况下,同样是差两个字,数值差却不同。
函数型
\(\sin (pos/x)\)——周期性函数
Sin的值域[-1,1],对于任意长度的文本,相同相对距离的词之间位置embedding的差值都是相同的。 然而x取值大,则波长大,导致相邻位置的差值变小。x取值过小,则对于长文本来说,很容易就走了几个波峰,导致不同距离,但差值相同。如何取合适的x是一个很关键的问题。
相对位置函数
在GPT-3论文中给出的公式如下:
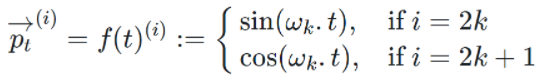
首先需要注意的是,上个公式给出的每一个Token的位置信息编码不是一个数字,而是一个不同频率分割出来,和文本一样维度的向量。向量如下:
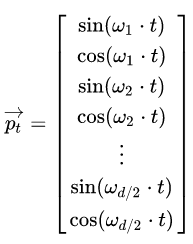
其中,\(t\)就是每个token的位置,比如说是位置1,位置2,以及位置n,而不同频率是通过\(w_i\)来表示的:
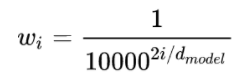
我们分别展开看\(pos\)和\(pos+k\)这两个字符的关系。按照位置编码的的公式,可以计算的位置编码,其结果如下:
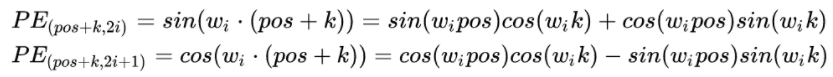
其中:
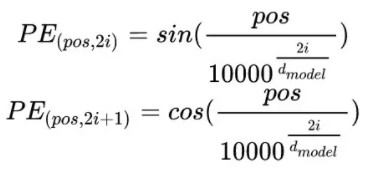
带入之后的结果如下:
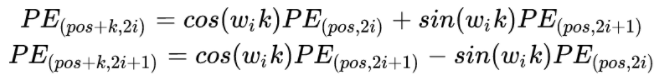
我们可以知道,距离K是一个常数,所有上面公式中和的计算值也是常数,可以表示为:
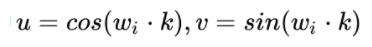
这样,就可以将写成一个矩阵的乘法:
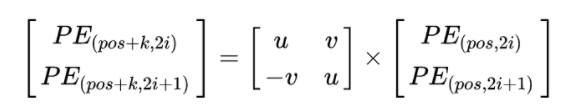
如上所述,该方法计算的相对位置是线性关系,但是位置的方向信息其实是丢失的,即\(PE_{pos+k}PE_{pos}=PE_{pos-k}PE_{pos}\)。
加入方向信息的相对位置函数
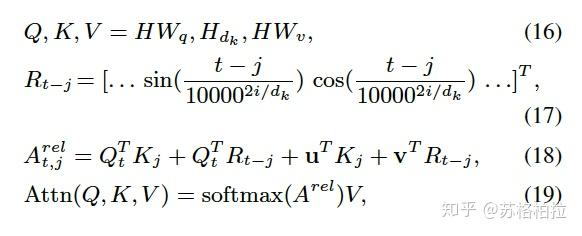
核心是公式(18),原始的self-attention是只有\(Q_t*K_j\),这里把位置信息也跟\(Q_t\)相乘了。且\(R_{t-j}\)的设定方式也决定它能反映出位置信息。假设\(t=5\),\(j\)分别为0,10,则\(t-j\)分别为5和-5。已知\(sin(-x)=-sin(x),cos(-x)=cos(x)\)。很明显,我们可以发现对于0和10,值是互为正反,通过这种方式把方向信息就学到了。
网络自行学习 positional encoding
把 positional encoding 里面的数值,当作神经网络参数的一部分,直接学习出来,如下图中右上角的可视化结果所示。
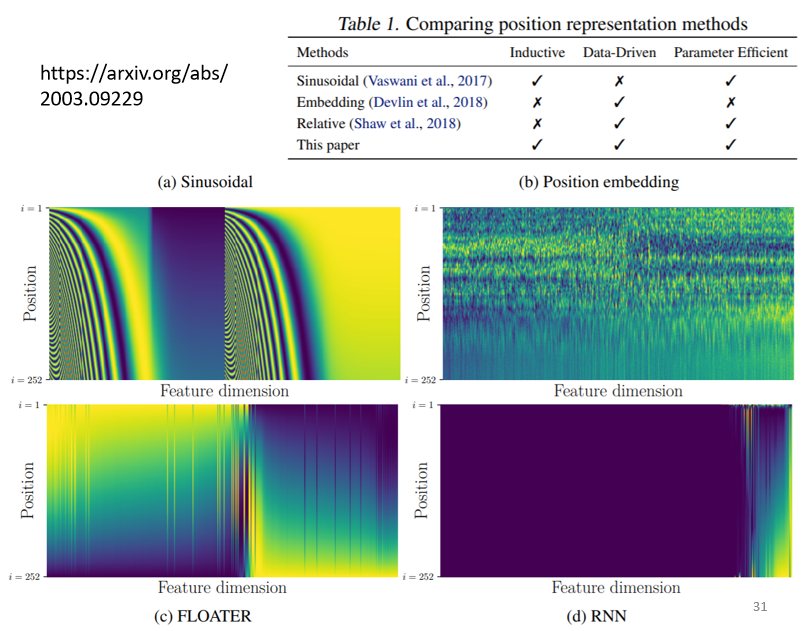
positional encoding仍然是一个尚待研究的问题,可以自己设计,核心是尽可能能为序列提供位置信息,比如满足前面提到的几个条件:保证值域固定,且不同长度文本,相差相同字数,差相同值,不同顺序(方向)含义不同。